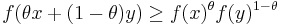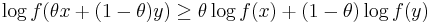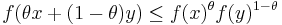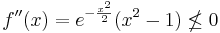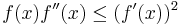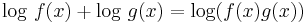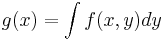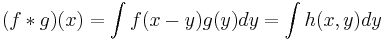Logarithmically concave function
In convex analysis, a non-negative function f : Rn → R+ is logarithmically concave (or log-concave for short) if its domain is a convex set, and if it satisfies the inequality
for all x,y ∈ dom f and 0 < θ < 1. If f is strictly positive, this is equivalent to saying that the logarithm of the function, log ∘ f, is concave; that is,
for all x,y ∈ dom f and 0 < θ < 1.
Examples of log-concave functions are the 0-1 indicator functions of convex sets (which requires the more flexible definition), and the Gaussian function.
Similarly, a function is log-convex if satisfies the reverse inequality
for all x,y ∈ dom f and 0 < θ < 1.
Contents |
Properties
- A positive log-concave function is also quasi-concave.
- Every concave function that is nonnegative on its domain is log-concave. However, the reverse does not necessarily hold. An example is the Gaussian function f(x) = exp(−x2/2) which is log-concave since log f(x) = −x2/2 is a concave function of x. But f is not concave since the second derivative is positive for |x| > 1:
- A twice differentiable, nonnegative function with a convex domain is log-concave if and only if for all x satisfying f(x) > 0,
-
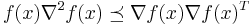 , [1]
, [1]
- i.e.
-
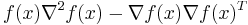 is
is
- negative semi-definite. For functions of one variable, this condition simplifies to
Operations preserving log-concavity
- Products: The product of log-concave functions is also log-concave. Indeed, if f and g are log-concave functions, then log f and log g are concave by definition. Therefore
- is concave, and hence also f g is log-concave.
- Marginals: if f(x,y) : Rn+m → R is log-concave, then
- is log-concave (see Prékopa–Leindler inequality).
- This implies that convolution preserves log-concavity, since is log-concave if f and g are log-concave, and therefore
- is log-concave.
Notes
- ^ Stephen Boyd and Lieven Vandenberghe, Convex Optimization (PDF) p.105
References
- Barndorff-Nielsen, Ole (1978). Information and exponential families in statistical theory. Wiley Series in Probability and Mathematical Statistics. Chichester: John Wiley \& Sons, Ltd.. pp. ix+238 pp.. ISBN 0-471-99545-2. MR489333.
- Dharmadhikari, Sudhakar; Joag-Dev, Kumar (1988). Unimodality, convexity, and applications. Probability and Mathematical Statistics. Boston, MA: Academic Press, Inc.. pp. xiv+278. ISBN 0-12-214690-5. MR954608.
- Pfanzagl, Johann; with the assistance of R. Hamböker (1994). Parametric Statistical Theory. Walter de Gruyter. ISBN 3-11-01-3863-8. MR1291393.
- Pečarić, Josip E.; Proschan, Frank; Tong, Y. L. (1992). Convex functions, partial orderings, and statistical applications. Mathematics in Science and Engineering. 187. Boston, MA: Academic Press, Inc.. pp. xiv+467 pp.. ISBN 0-12-549250-2. MR1162312.